Advent of Code 2020 - Day 24, in Kotlin - Lobby Layout • Todd Ginsberg

Today’s puzzle reminds me of the code we wrote for Advent of Code 2020 Day 17 , except with a hex grid. We also had a hex puzzle in Advent of Code 2017 Day 11 (“Hex Ed”), and I used this wonderful page maintained by Red Blog Games to learn about hex grids. I wonder if they notice a large spike in traffic every time Advent of Code does a hex grid puzzle?

Solving the puzzle today was a nice way to spend a rainy Christmas eve morning.

If you’d rather just view code, the GitHub Repository is here .

Problem Input

We will take our input in as a List<String> and set it as a property on our daily solution class. We’ll parse it in part 1.

class Day24(private val input: List<String>)

⭐ Day 24, Part 1

The puzzle text can be found here.

Before we start coding, I want to discuss how we’ll represent our hexagonal grid. While it is possible to represent a hexagonal grid as a set of 2D points, I find it mentally easier to deal with the 3D or cube representation:

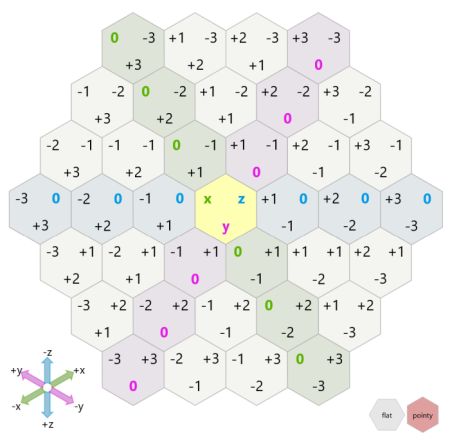
Hexagonal grid expressed as a cube — Image courtesy of Red Blob Games

This means we’ll be altering our existing Point3D class to account for its hexagonal neighbors.

// Point3D

companion object {
    val ORIGIN = Point3D(0, 0, 0)
    val HEX_OFFSETS = mapOf(
        "e" to Point3D(1, -1, 0),
        "w" to Point3D(-1, 1, 0),
        "ne" to Point3D(1, 0, -1),
        "nw" to Point3D(0, 1, -1),
        "se" to Point3D(0, -1, 1),
        "sw" to Point3D(-1, 0, 1),
    )
}

The first thing we’ll add are some frequently used constants. We’ll add an ORIGIN (or starting point) and an offset for each of the hexagonal neighbors. I used the chart above to figure out the changes in x, y, and z.

Because those are offsets, we’ll need to be able to add Point3D objects together easily. Luckily, we can override + in Kotlin, so we’ll write some code to do that:

// In Point3D

operator fun plus(other: Point3D): Point3D =
    Point3D(x + other.x, y + other.y, z + other.z)

That code should look very similar to the code we wrote in Point2D to do the same thing.

Next, we need to add is a way to get the hexagonal neighbor of a given Point3D, by its direction name. We’ll use the same directions that the problem input from today uses, and apply the offset to the current Point2D to get the desired neighboring spot. We’ll throw an exception if somebody hands us a direction we aren’t expecting.

// In Point3D

fun hexNeighbor(dir: String): Point3D =
    if (dir in HEX_OFFSETS) HEX_OFFSETS.getValue(dir) + this
    else throw IllegalArgumentException("No dir: $dir")

Now we can start solving our puzzle. The first thing we need to do is walk a path, and return the final element. This is the part that messed me up for a while, I didn’t read the instructions properly and was keeping every tile along the path, not just the ones that I had ended up on. We’ll implement walkPath as an extension on String, and it will return the final Point3D along that path.

// In Day24

private fun String.walkPath(): Point3D =
    splitPattern
        .findAll(this)
        .map { it.value }
        .fold(Point3D.ORIGIN) { last, dir ->
            last.hexNeighbor(dir)
        }

companion object {
    private val splitPattern = "([ns]?[ew])".toRegex()
}

We parse our input using a Regular Expression, which I have defined in the companion object. We split our input String and findAll the matches that our regular expression will generate. Because the findAll function returns a Sequence<MatchResult>, we only care about the values it finds, so we map them and pass them to a fold. The fold is used to iterate over all of the directions and to build up a path as we go. A fold is nice here because we can tell it we’re starting with the ORIGIN, and carry forward the latest point on the path that we’ve looked at.

Now that we can walk a single path, we need a function to walk every path and keep track of which tiles we’ve passed over and how many times:

// In Day24

private fun decorateFloor(): Set<Point3D> =
    input
        .map { it.walkPath() }
        .groupBy { it }
        .filter { it.value.size % 2 == 1  }
        .keys

In the decorateFloor function, we call walkPath on each line of input (our paths). When we have all of the Point3D objects from all of the paths, we group them together by calling groupBy { it }, which will give us a Map<Point3D, List<Point3D>>. If we filter out the points that we have seen an odd number of times, that will give us a map whose keys represent black tiles. We return a Set<Point3D> which contains only black tiles to the caller.

And now we can solve part 1!

// In Day24

fun solvePart1(): Int =
    decorateFloor().size

Because decorateFloor only returns the black tile points, we can get the size of that for our answer!

Star earned! Onward!

⭐ Day 24, Part 2

The puzzle text can be found here.

Ah! Game of life but with hex tiles instead of squares. The first thing we’ll need is a way to lazily get the hexagonal neighbors of a Point3D. We make this use the lazy delegate for two reasons. First, if we make this a value property, it will evaluate when we create a Point3D, leading to an infinite loop. Second, if we use lazy, the result is cached for us. So if we end up calling hexNeighbors for the same point more than once, we’ve saved a bit of time.

// In Point3D

val hexNeighbors: List<Point3D> by lazy {
    HEX_OFFSETS.map { this + it.value }
}

To calculate all of the hex neighbors for a given point, we add the offsets we have defined previously.

And once we have that, we can mutate the floor according to the puzzle rules. We have a Set<Point3D> so we’ll implement nextFloor as an extension function that returns another Set<Point3D>

// In Day24

private fun Set<Point3D>.nextFloor(): Set<Point3D> {
    val pointsToEvaluate = this + (this.flatMap { point -> point.hexNeighbors })
    return pointsToEvaluate.filter { tile ->
        val adjacentBlackTiles = tile.hexNeighbors.count { it in this }
        val black = tile in this
        when {
            black && (adjacentBlackTiles == 0 || adjacentBlackTiles > 2) -> false
            !black && adjacentBlackTiles == 2 -> true
            else -> black
        }
    }.toSet()
}

To properly calculate the next floor, we need to know all of the points we care about. These are stored in pointsToEvaluate and it is made up of all the spots currently in the set (all of the black tiles we have) and all of their neighbors. We can add those by flatmapping each point to all of its neighbors.

We calculate the next floor by applying the rules to each point. We count up how many adjacentBlackTiles each point has and whether a given tile is black or white (whether it is in the original set, not the pointsToEvaluate). We return those points as a Set<Point3D>, which represents black tiles in the next iteration of the floor.

And now we can solve part 2!

We’ll use generateSequence to keep producing the nextFloor for as long as we need it. Because we don’t need any intermediate results, we drop the first 100 rounds (not 99! We have to account for the 0th floor, the starting point from decorateFloor, which does not count for the 100 days). Taking the next (101st) floor configuration via first will give us our answer, and we return its size like we did in part 1.

// In Day24

fun solvePart2(): Int =
    generateSequence(decorateFloor()) { it.nextFloor() }
        .drop(100)
        .first()
        .size

Star earned! I’ll see you tomorrow for the last day of Advent of Code 2020! :(

⭐ Day 24, Part 1

⭐ Day 24, Part 2

Further Reading